Visual Group Theory

Data: 1.09.2018 / Rating: 4.8 / Views: 854

Gallery of Video:

Gallery of Images:

Visual Group Theory - DOWNLOAD

Visual Group Theory

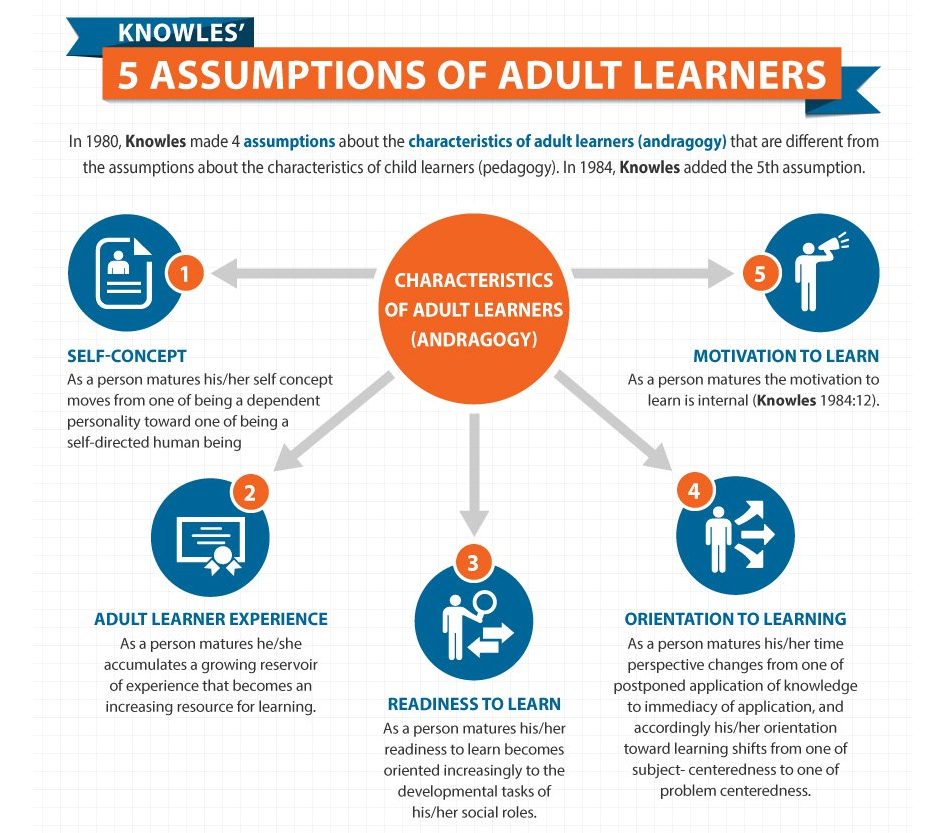
Many people find group theory pretty difficult because the logic behind it seems algebraic to the extreme and geometric not at all. However, there are a few ways to Visual Group Theory assumes only a high school mathematics background and covers a typical undergraduate course in group theory from a thoroughly visual perspective. The more than 300 illustrations in Visual Group Theory bring groups, subgroups, homomorphisms, products, and. In short, the answer is: group theory is the systematic study of symmetry. When a physical system or mathematical structure possesses some kind of. Visual Group Theory is his first book, based on lessons learned while writing the software Group Explorer. Like several of his research projects, it puts computers to work to improve mathematical understanding and education. Nathan Carter's colorful text, Visual Group Theory, approaches the learning of group theory visually. Its topics and theorems are accompanied by visual demonstrations of the meaning and importance of groups, from the basics of groups and subgroups through advanced structural concepts such as semidirect products and Sylow theory. Visual Group Theory (MAA Classroom Resource Materials) (MAA Problem Book Series): Nathan Carter: : Amazon. com: Books Download visual group theory ebook free in PDF and EPUB Format. visual group theory also available in docx and mobi. Read visual group theory online, read in mobile or Kindle. matggroup theory download free. Finding books BookSee BookSee Download books for free. Find books Visual Group Theory Nathan C. Carter First and foremost, images and visual examples are the heart of this book. There are more than 300 images, an average of more than one per page. The most used visualization tool is Cayley diagrams (definedin Chapter 2) because they represent group structure Group theory is the branch of mathematics that studies symmetry, found in crystals, art, architecture, music and many other contexts. But its beauty is lost on students when it is taught in a technical style that is difficult to understand. Visual Group Theory assumes only a high school mathematics background and covers a typical undergraduate course in group theory from a thoroughly visual perspective. The more than 300 illustrations in Visual Group Theory bring groups, subgroups, homomorphisms, products, and. Visual Group Theory assumes only a high school mathematics background and covers a typical undergraduate course in group theory from a thoroughly visual perspective. Group theory, in modern algebra, the study of groups, which are systems consisting of a set of elements and a binary operation that can be applied to two elements of. Visual Group Theory assumes only a high school mathematics background and covers a typical undergraduate course in group theory from a Group theory is the branch of mathematics that studies symmetry, found in crystals, art, architecture, music and many other contexts. Symmetry, Automorphisms, and Visual Group Theory. From the conclusion of Weyl's Symmetry. One example of Weyl's structureendowed entity is a partition of a sixelement set into three disjoint twoelement sets for instance, the partition of the six faces of a cube into three pairs of opposite faces. GROUP THEORY: A FIRST JOURNEY VIPUL NAIK Abstract. Group theory is an important topic in most undergraduate math curricula, and forms the basis for higher studies both in math and in areas where math is applied. Group theory is the branch of mathematics that studies symmetry, found in crystals, art, architecture, music and many other contexts, but its beauty is lost on students when it is taught in a technical style that is difficult to understand. The solutions use a variety of methods of modern mat matics, including convex and combinatorial geometry, coding theory, calculus of variations, di erential geometry, group theory, and topology, as well as geometric analysis and number theory. We work on fundamental problems in mathematics and theoretical computer science, interact extensively with the academic community and collaborate with other researchers at MSR on challenging applied problems. Among our areas of expertise are probability, algorithms, statistical learning, optimization, algorithmic game theory, errorcorrecting codes, combinatorics, statistical physics, and. [Nathan C Carter This text approaches the learning of group theory visually. It allows the student to see groups, experiment with groups and understand their significance. It brings groups, subgroups, homomorphisms. PRACTICE VISUAL GROUP THEORY ANSWERS Each of the graphs below was created by the program Group Explorer. Draw a Cayley graph for D4, the group of symmetries of the square. Draw a Cayley graph for each of the abelian groups below of order 4. Visual Group Theory assumes only a high school mathematics background and covers a typical undergraduate course in group theory from a thoroughly visual perspective. The more than 300 illustrations in Visual Group Theory bring groups, subgroups, homomorphisms, products, and. Visual Group Theory is his first book, based on lessons learned while writing the software Group Explorer. Like several of his research projects, it puts computers to work to improve mathematical understanding and education. Class begins on Monday, July 13. Throughout the course, we will be using software called Group Explorer, which compliments our textbook Visual Group Theory. The software is free and works on all operating systems. A book designed to be used alone or in conjunction with Group Explorer, giving a thoroughly visual introduction to group theory, building strong intuition for the mathematical objects called groups. Visual Group Theory is his first book, based on lessons learned while writing the software Group Explorer. Like several of his research projects, it puts computers to work to improve mathematical understanding and education. This note covers the following topics: Notation for sets and functions, Basic group theory, The Symmetric Group, Group actions, Linear groups, Affine Groups, Projective Groups, Finite linear groups, Abelian Groups, Sylow Theorems and Applications, Solvable and nilpotent groups, pgroups, a second look, Presentations of Groups, Building new groups from old. The following figure (taken from page 28 of Visual Group Theory) depicts a molecule of Boric acid. chemists use group theory to classify their shapes. Follow the steps of Definition 3. I love the Visual Group Theory (VGT) approach of introducing the concept of a group first using the Rubik's cube, and then Cayley diagrams, the latter of which is a common theme throughout the course. For someone new to Group theory this will cause major (and unnecessary) confusion. So, while I appreciate the author's effort to take a more visual approach to group theory, I. Visual Group Theory assumes only a high school mathematics background and covers a typical undergraduate course in group theory from a thoroughly visual perspectiv e. , The more than 300 illustrations in Visual Group Theory bring groups, subgroups, homomorphisms, products, and. Visual Group Theory assumes only a high school mathematics background and covers a typical undergraduate course in group theory from a thoroughly visual perspective. The more than 300 illustrations in Visual Group Theory bring groups, subgroups, homomorphisms, products, and. Visual Group Theory Group theory is the branch of mathematics that studies symmetry, found in crystals, art, architecture, music and many other contexts, but its beauty is lost on students when it is taught in a technical style that is difficult to understand. This item will be released on 15 October 2018. Visual Group Theory, Lecture 1. In this lecture, we will introduce the concept of a group using the famous Rubik's cube. The formal definition will be given later, in Lecture 1. Artin's Book would provide a great reference text for a refresh but it covers a lot of areas, and you sometimes lack the motivation to study the area without seeing it from a book devoted to it or from seeing it occur naturally. Free PDF Download Books by Nathan Carter. This text approaches the learning of group theory visually. It allows the student to see groups, experiment with groups and understand their significance. It Group theory has three main historical sources: number theory, the theory of algebraic equations, and geometry. The numbertheoretic strand was begun by Leonhard Euler, and developed by Gauss's work on modular arithmetic and additive and multiplicative groups related to quadratic fields. This text approaches the learning of group theory visually. It allows the student to see groups, experiment with groups and understand their significance. It brings groups, subgroups, homomorphisms, products, and quotients into clear view. Every topic and theorem is accompanied with a visual demonstration of its meaning and import, from the basics of groups and subgroups through advanced. Visual group theory, by Nathan Carter. Groups and Symmetries: From Finite Groups to Lie Groups, by Yvette KosmannSchwarzbach. Lie Groups: An Approach through Invariants and Representations, by. However, Nathan Carters Visual Group Theory, published this summer by the MAA, has done just that. To be precise, Carters book is not a full abstract algebra book but rather a book about group theory with a few topics about fields covered at the end. This text approaches the learning of group theory visually. It allows the student to see groups, experiment with groups and understand their significance. It brings groups, subgroups, homomorphisms, products, and quotients into clear view. Every topic and theorem is accompanied with a visual demonstration of its meaning and import, from the basics of groups and subgroups through advanced. Group theory is the branch of mathematics that studies symmetry, found in crystals, art, architecture, music and many other contexts. But its beauty is lost on students when it is taught in a technical style that is difficult to understand. Visual Group Theory is his first book, based on lessons learned while writing the software Group Explorer. Like several of his research projects, it puts computers to work to improve mathematical understanding and education.

Related Images:

Similar articles:

....